PERSAMAAN HARGA MUTLAK

Nilai mutlak dari suatu bilangan x dapat diartikan sebagai jarak bilangan tersebut terhadap titik 0 pada garis bilangan, dengan tidak memperhatikan arahnya.

Ini berarti |x| = 5 memiliki dua selesaian, karena terdapat dua bilangan yang jaraknya terhadap 0 adalah 5 yaitu  x = –5 dan x = 5 (perhatikan gambar berikut).

   Untuk lebih jelasnya perhatikan beberapa contoh soal berikut ini :
      A.  Tentukan nilai x yang memenuhi persamaan berikut :

      (a) │2x – 5│ = 3                               (b) │4 – 3x│ = 6 

 

      Pembahasan :

       (a)                   │2x – 5│ = 3

                  (2x – 5)² = 3²

         4x² – 20x + 25 = 9

         4x² – 20x + 16 = 0

               x² – 5x + 4 = 9

           (x – 4)(x – 1) = 0             Jadi x = 1 dan x = 4

       

       (b)             │3 – 2x│ = 7

              (3 – 2x)² = 7²

       9 – 12x + 4x² = 49

     4x² – 12x – 40 = 0

         x² – 3x – 10 = 0

       (x – 5)(x + 2) = 0                 Jadi x = 5 atau x = –2

      B.  Tentukan nilai x yang memenuhi persamaan berikut :

      (a)│2x + 4│ = │x – 1│                    (b) │3x + 4│ = │2x – 1│


      Pembahasan :
       (a)               │2x + 4│ = │x – 1│

                (2x + 4)² = (x – 1)²

        4x² –16x + 16 = x² – 2x + 1

       3x² – 14x + 15 = 0

       (3x – 5)(x – 3) = 0              Jadi x = 5/3 atau x = 3

        
        (b)             │3x + 4│ = │2x – 1│

               (3x + 4)² = (2x – 1)²

       9x² +24x + 16 = 4x² – 4x + 1

      5x² + 28x + 15 = 0

      (5x + 3)(x + 5) = 0               Jadi x = –3/5 atau x = –5

     C. Tentukan nilai x yang memenuhi persamaan berikut :

      (a) |3x – 2│ = x + 4                         (b) │2x + 4│ = x – 3

     Pembahasan :
      (a)               │3x – 2│ = x + 4

               (3x – 2)² = (x + 4)²

        9x² – 12x + 4 = x² + 8x + 16

      8x² – 20x – 12 = 0

          2x² – 5x – 3 = 0

      (2x + 1)(x – 3) = 0            Jadi x = –1/2 atau x = 3

       Uji : x = –1/2 maka x + 4 = –1/2 + 4 = 7/2 (memenuhi)

       Uji : x = 3 maka x – 4 = 3 + 4 = 7 (memenuhi)

      

    Sehingga H = {–1/2, 3}

(b)       │2x – 4│ = x – 3

              (2x – 4)² = (x – 3)²

        4x² –16x + 16 = x² – 6x + 9

         3x² – 22x + 7 = 0

       (3x – 1)(x – 7) = 0                 Jadi x = 1/3 atau x = 7

Uji: x = 1/3 maka x – 3 = 1/3 – 4 = –11/3 (tidak memenuhi)

Uji: x = 7 maka x – 4 = 7 – 4 = 3 (memenuhi)

Sehingga H = {7}

 
  

    Selesaikan persamaan: –5|x – 7| + 2 = –13.

    Pembahasan





    
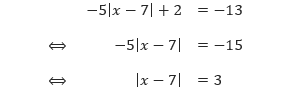
    Sekarang perhatikan bahwa x – 7 merupakan “X” pada sifat persamaan nilai mutlak,   
    sehingga



    
    Dengan mensubstitusi ke persamaan semula akan memastikan bahwa himpunan 
    selesaiannya adalah {4, 10}.

Kalo kalian belum puas coba kerjakan latihan berikut ini  :

 

 

Untuk melihat pembahasan soal bisa di download di sini

(Pembahasan) Soal PERSAMAAN Harga Mutlak

Ok guys....terima kasih telah mengunjungi blog kami dan semoga bisa bermanfaat... tunggu postingan kami berikutnya...